There are easy and simple step by step solutions you can use to solve row echelon form examples 3×3.
When working with systems of linear equations, Row Echelon Form (REF) is a crucial concept in matrix algebra. A matrix is in row echelon form when:
- All nonzero rows are above any rows of all zeros.
- Each leading entry (first nonzero number in a row) is to the right of the leading entry in the row above.
- The leading entries are not required to be 1, but zeros must appear below each leading coefficient.
Learning row echelon form through examples is one of the best ways to understand matrix row reduction.
By breaking it down step by step, you can see how different row operations help transform a matrix into REF, making it easier to solve linear systems.
If you’re looking for a quick way to check your work, you can use an online tool like the Matrix Row Reduction Calculator to perform row operations instantly.
For a deeper dive into Reduced Row Echelon Form (RREF)—a more refined version of REF—check out our guide on how to calculate RREF step by step.
Step 1: Define the Rules of Row Echelon Form
Before we begin solving, let’s clearly define the key rules a matrix must follow to be in Row Echelon Form (REF):
Leading Coefficients Must Be 1
- The first nonzero entry in each row (called a pivot) should ideally be 1. However, this is not strictly required for REF—only for RREF.
All Zeros Must Be Below Leading Coefficients
- Each leading coefficient should appear to the right of the leading coefficient in the row above. Any zeros must be placed below these pivots.
Rows with All Zeros Go at the Bottom
- If a row consists entirely of zeros, it must be placed at the bottom of the matrix.
By following these rules, we can systematically transform any matrix into REF using row operations.
Step 2: Example of Converting a 3×3 Matrix to REF
Let’s take a 3×3 matrix and convert it into Row Echelon Form step by step using row operations:
Step 2.1: Make the First Pivot 1
To create a leading 1 in the first column, we can swap row 1 and row 2:
Step 2.2: Eliminate Below the First Pivot
To create zeros below the first pivot (1 in row 1, column 1), we perform the following row operations:
Resulting matrix:
Step 2.3: Make the Second Pivot 1
Divide row 2 by -2 to create a 1 in the second pivot position:
Step 2.4: Eliminate Below the Second Pivot
To create a zero below the second pivot (row 3, column 2), we perform:
Final Row Echelon Form (REF):
At this point, the matrix is in Row Echelon Form!
To verify your steps, try using the Matrix Row Reduction Calculator and compare the result.
Step 3: How to Check if a Matrix is in REF
To confirm that your matrix is in Row Echelon Form, review the following checklist:
✅ Leading coefficients are positioned correctly (each one appears to the right of the one above).
✅ Zeros are below the leading coefficients in each column.
✅ Any all-zero rows are at the bottom of the matrix.
Common Mistakes to Avoid
❌ Forgetting to move an all-zero row to the bottom.
❌ Having a leading coefficient that is not to the right of the row above.
❌ Skipping necessary row swaps or not simplifying correctly.
By understanding these steps, you’ll be able to confidently convert any 3×3 matrix into REF and recognize common errors along the way!
Step 4: Using a Calculator to Solve More Row Echelon Form Examples 3×3 Matrices
While solving matrices by hand is a great way to build a strong understanding of row echelon form, using a calculator can help verify your results and save time—especially for larger matrices.
How to Use the Matrix Row Reduction Calculator
Let’s walk through solving a 3×3 matrix using the Matrix Row Reduction Calculator:
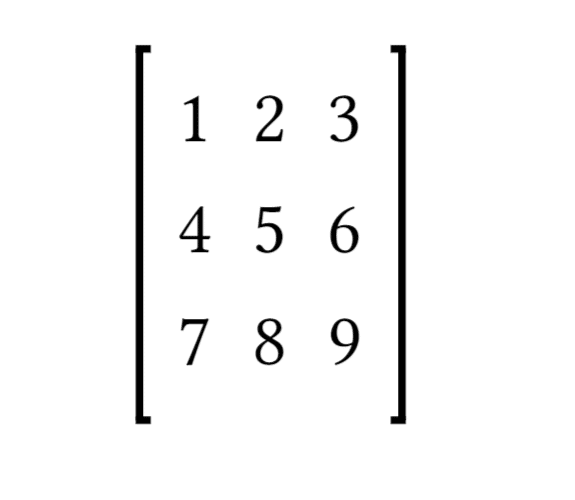
Enter the Matrix
- Open the calculator and input your 3×3 matrix values into the designated fields.
- Example:

Perform Row Reduction
- Click the “Calculate” button.
- The calculator will apply row operations and display the row echelon form (REF) of the matrix step by step.
Compare Your Work
- Check if your manual solution matches the calculator’s result.
- If there’s a difference, review your row operations to spot any mistakes.
Why Use a Calculator?
✔️ Instant verification – Check your solutions without lengthy calculations.
✔️ Step-by-step breakdown – See how the matrix is reduced to REF.
✔️ Practice with different matrices – Experiment with various inputs to deepen your understanding.
For a more advanced transformation, where the leading coefficients are all 1s and the matrix is in its most reduced form, you may also want to learn about Reduced Row Echelon Form (RREF) in our previous guide!
Now that you know how to solve 3×3 row echelon form examples both manually and with a calculator, try reducing a few matrices on your own to sharpen your skills!
Conclusion
Mastering Row Echelon Form (REF) is an essential step in understanding matrix row reduction and solving systems of linear equations. In this guide, we covered:
✅ The key rules that define REF
✅ A step-by-step example of converting a 3×3 matrix to REF
✅ How to check if a matrix is correctly reduced
✅ Common mistakes to avoid
✅ How to use the Matrix Row Reduction Calculator to verify your results
By practicing these steps, you’ll develop a strong intuition for matrix transformations and row operations. If you’re ready to take your skills further, explore our guide on Reduced Row Echelon Form (RREF) to see how matrices can be fully simplified for solving equations.
Now, try solving a few row echelon form examples 3×3 matrices on your own and use the calculator to check your work. The more you practice, the easier matrix row reduction will become!

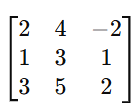
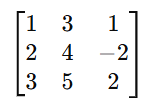
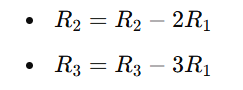
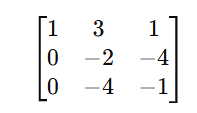
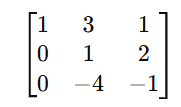
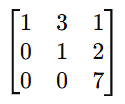
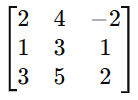
Be First to Comment