Solving systems of equations manually can be time-consuming, especially when working with large matrices. Fortunately, a Reduced Row Echelon Form Calculator simplifies the process by providing quick and accurate solutions.
What is Reduced Row Echelon Form?
Reduced Row Echelon Form (RREF) is a special type of matrix form where:
- Each leading coefficient (pivot) is 1 and appears to the right of the one in the row above.
- All other elements in the pivot column are zero.
- Any rows consisting entirely of zeros are placed at the bottom.
This standardized form makes it easy to interpret solutions to systems of equations, identify dependent and independent variables, and determine the rank of a matrix.
Why Use a Reduced Row Echelon Form Calculator?
While row reduction can be done by hand using Gaussian or Gauss-Jordan elimination, a reduced row echelon form calculator (RREF calculator) significantly speeds up the process by:
✔ Eliminating human error.
✔ Handling large matrices efficiently.
✔ Providing step-by-step solutions for learning and verification.
You can use the RREF Calculator, which allows you to quickly reduce any matrix to reduced row echelon form.
For a deeper understanding of RREF, you might find these related guides helpful:
- Rules for Reduced Row Echelon Form – Learn the key principles behind RREF.
- Row Echelon Form vs. Reduced Row Echelon Form – Understand the difference between these two echelon forms.
Now, let’s explore the rules of RREF. 🚀
Understanding the Rules of Reduced Row Echelon Form
Before using a Reduced Row Echelon Form (RREF) calculator, it’s important to understand the key rules that define RREF.
These rules ensure that the matrix is in its simplest form, making it easy to extract solutions.
Rules for a Matrix to Be in Reduced Row Echelon Form
A matrix is in Reduced Row Echelon Form if it meets the following conditions:
1️⃣ Leading Coefficients Must Be 1
- Each nonzero row has a leading coefficient (pivot) of 1.
- This leading 1 is called a pivot and must be placed correctly in each row.
2️⃣ Zeros Above and Below Each Leading 1
- Every column containing a leading 1 must have all other elements as zero (both above and below).
- This step fully simplifies the matrix, making it easier to interpret.
3️⃣ Each Leading 1 Must Be to the Right of the One Above It
- The pivot position in each row must move rightward as you move down the matrix.
4️⃣ Rows with All Zeros Go at the Bottom
- Any row that consists entirely of zeros must be moved to the bottom of the matrix.
Following these rules ensures that a system of equations is in its simplest, most interpretable form.
Row Echelon Form vs. Reduced Row Echelon Form
Both Row Echelon Form (REF) and Reduced Row Echelon Form (RREF) simplify matrices, but there is an important distinction between them:
| Feature | Row Echelon Form (REF) | Reduced Row Echelon Form (RREF) |
|---|---|---|
| Leading 1s (pivots) | Must be to the right of the previous row’s leading 1 | Same as REF |
| Zeros below pivots | Required | Required |
| Zeros above pivots | Not required | Required (full reduction) |
| Solution Interpretation | May require back-substitution | Solutions can be read directly |
When to Use REF vs. RREF?
- REF is useful as an intermediate step in solving equations using Gaussian elimination.
- RREF is preferred for final solutions, especially in Gauss-Jordan elimination and software applications.
If you want to quickly reduce a matrix to RREF and verify your work, try the Row Reduction Calculator for step-by-step solutions!
For more insights, check out:
- Solve System of Equations Using Row Reduction – Learn how to use row reduction to solve linear systems.
Next, let’s look at how to use an RREF calculator effectively. 🚀
How an Reduced Row Echelon Form Calculator Works
Using a reduced row echelon form calculator simplifies the row reduction process by performing all calculations instantly.
Instead of manually applying row operations, the calculator automates each step, ensuring accuracy and efficiency.
Step-by-Step Process Used in a RREF Calculator
1️⃣ Input the Matrix
- Enter the matrix into the calculator.
- The matrix should be in augmented form if solving a system of equations.
2️⃣ Apply Row Operations Automatically
- The calculator follows the Gaussian elimination process to transform the matrix into Row Echelon Form (REF).
- It then applies Gauss-Jordan elimination to convert the matrix to Reduced Row Echelon Form (RREF).
3️⃣ Generate the Final RREF Matrix
- The result is displayed in RREF format, where:
✔ Leading coefficients are 1.
✔ Zeros appear above and below each pivot.
✔ Any zero rows are at the bottom of the matrix.
4️⃣ Interpret the Solution
- If the matrix represents a system of equations, the final RREF form provides:
- Unique solution (if each variable has a pivot column).
- Infinite solutions (if a row of all zeros appears with a free variable).
- No solution (if a contradictory row like
[0 0 0 | 1]appears).
Manual Row Reduction vs. Calculator Results
| Feature | Manual Row Reduction | RREF Calculator |
|---|---|---|
| Time Required | Can be slow, especially for large matrices | Instant results |
| Accuracy | Prone to human error | 100% accurate |
| Step-by-Step Process | Must track each row operation | Automatically applied |
| Application | Great for learning concepts | Useful for quick verification |
A reduced row echelon form calculator, like the reduced echelon form calculator, is especially helpful for students and professionals working with complex matrices.
Example Calculations Using the Reduced Row Echelon Form Calculator
To demonstrate how an RREF calculator works, let’s go through three example problems.
We will input a matrix, apply row reduction using the RREF Calculator, and interpret the results.
Example 1: Simple 2×2 Matrix
Consider the following 2×2 system of equations:
Step 1: Convert to Augmented Matrix
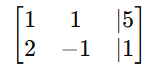
Step 2: Apply Row Operations
- Multiply row 1 by -2 and add it to row 2:
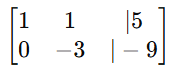
- Divide row 2 by -3 to make the pivot 1:
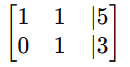
- Subtract row 2 from row 1:
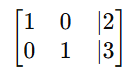
Using the calculator, we reduce the matrix to RREF form:
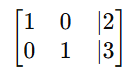
Step 3: Interpret the Solution
From this, we conclude:
![]()
Example 2: 3×3 System Solving for Variables
Consider the following system of equations:
Step 1: Convert to Augmented Matrix
Step 2: Apply Row Reduction
- Subtract 2 × row 1 from row 2.
- Subtract 3 × row 1 from row 3.
- Multiply row 2 by -1 to make the pivot positive:
- Add 5 × row 2 to row 3:
- Divide row 3 by 18 to get a leading 1:
- Subtract 5 × row 3 from row 2.
- Subtract 3 × row 3 from row 1.
- Subtract 2 × row 2 from row 1:
Using the calculator, the final RREF form is:
Step 3: Interpret the Solution
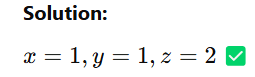
This means the system has a unique solution.
Example 3: Larger 4×4 Matrix with Dependent Equations
Consider this system:
Step 1: Convert to Augmented Matrix
Step 2: Apply Row Reduction
The RREF form is:
Step 3: Interpret the Solution
Since we have a row of all zeros, the system has infinitely many solutions. This means one or more variables are free, leading to multiple solutions.
Try It Yourself!
Use the reduced row echelon calculator to input your own matrices and check their RREF forms. If you’re new to row reduction, check out:
- Rules for Reduced Row Echelon Form – Learn the key properties of RREF.
- Calculate Reduced Row Echelon Form – Step-by-step guide to solving equations with RREF
Features of a Good Reduced Row Echelon Form Calculator
When choosing a Reduced Row Echelon Form (RREF) calculator, it’s important to look for certain features that enhance usability and accuracy.
Here are the key aspects of a high-quality reduced row echelon form calculator:
1. Step-by-Step Solution Breakdown
A good calculator doesn’t just give the final answer—it shows each row operation used to reach RREF. This helps students and professionals understand the process instead of just memorizing results.
🔹 Why It Matters: Learning through step-by-step solutions reinforces matrix row reduction concepts.
🔹 Example: The Matrix Row Reduction Calculator provides a clear breakdown of every transformation.
2. Supports Custom Row Operations
Advanced users may want to apply specific row operations manually instead of relying solely on automation. A great calculator should allow:
✅ Row swapping (switching two rows).
✅ Scaling (multiplying a row by a nonzero number).
✅ Row replacement (adding/subtracting multiples of rows).
🔹 Why It Matters: This flexibility is helpful for teaching purposes and for verifying manual calculations.
3. Fast and Accurate Calculations
A high-quality RREF calculator should be optimized for speed and precision, especially for large matrices (4×4, 5×5, or higher).
🔹 Why It Matters: In fields like engineering, physics, and data science, complex matrices need fast and accurate computation.
4. User-Friendly Interface
A simple and clean design makes it easier for users to enter matrices and interpret results.
🔹 Key Features to Look For:
- Easy-to-use matrix input system.
- Clearly labeled output showing RREF.
- Support for fractions or decimals.
💡 Want to see these features in action? Try the Row Echelon Calculator !
How to Use the Reduced Row Echelon Form Calculator
If you’re looking for a fast and accurate way to compute Reduced Row Echelon Form (RREF), the Row Reduction Calculator is a great tool.
It simplifies matrices step by step, making it easier to understand the row reduction process.
Step-by-Step Guide to Using the Reduced Row Echelon Form Calculator
1. Enter the Matrix Dimensions
- Go to MatrixRowReductionCalculator.com.
- Choose the number of rows and columns for your matrix (e.g., a 3×3 or 4×4 matrix).
2. Input Your Matrix Values
- Enter each number into the corresponding cell of the matrix grid.
3. Click “Calculate”
- The tool will perform Gaussian elimination followed by Gauss-Jordan elimination to reduce the matrix to RREF.
- You’ll see step-by-step transformations, helping you understand how each row operation affects the matrix.
- The output will display the matrix in RREF format.
💡 Why Use This Calculator?
✔ Saves time by automating row reductions.
✔ Shows step-by-step solutions for learning purposes.
✔ Handles matrices of various sizes efficiently.
Real-World Applications of Using RREF in Mathematics and Science
The Reduced Row Echelon Form (RREF) of a matrix is more than just a theoretical concept—it has practical applications in various fields of mathematics, science, and engineering.
By transforming matrices into a simplified form, RREF allows for easier problem-solving in many real-world scenarios.
1. Solving Systems of Linear Equations
One of the most common applications of RREF is in solving systems of equations. Many problems in physics, engineering, and economics require solving multiple equations simultaneously.
- Example: In circuit analysis, Kirchhoff’s laws generate a system of equations that can be solved using RREF.
- RREF provides a direct solution, reducing manual calculations and errors.
2. Determining Matrix Rank and Linear Independence
- The rank of a matrix is the number of nonzero rows in its RREF.
- Rank is crucial for understanding linear dependence in vector spaces, which is widely used in machine learning and data science.
- In computer graphics, linear independence helps determine transformations like rotations and scaling in 3D modeling.
3. Finding the Inverse of a Matrix
- The inverse of a matrix is required in cryptography, physics, and economics.
- By augmenting a matrix with the identity matrix and applying RREF, we can compute the inverse efficiently.
- Example: In cryptography, some encryption methods rely on matrix inverses for encoding and decoding messages.
4. Applications in Statistics and Data Science
- In regression analysis, RREF is used to solve least squares problems, which find the best-fit line or model for a dataset.
- Principal Component Analysis (PCA), a technique in machine learning, relies on linear algebra concepts like eigenvalues, eigenvectors, and row reduction.
5. Physics and Engineering Applications
- Quantum mechanics: Matrices are used to describe quantum states, and row reduction helps in simplifying calculations.
- Structural engineering: RREF is used in finite element analysis (FEA) to model stress and strain in materials.
- Control systems: Engineers use row reduction to analyze system stability and optimize control functions.
Try It Yourself
If you want to experiment with RREF and see how it applies to your field, try the Echelon Form Calculator.
It provides step-by-step solutions, making complex problems easier to understand and solve.
Now that we’ve explored real-world applications, let’s wrap up with a final conclusion on the importance of RREF.🚀
Conclusion
The Reduced Row Echelon Form (RREF) is a powerful tool in linear algebra, making it easier to solve systems of equations, analyze matrix properties, and apply mathematical concepts to real-world problems.
Whether you’re working in engineering, physics, computer science, or data analytics, understanding RREF is essential for simplifying complex calculations.
Using an RREF calculator can significantly save time and reduce errors, allowing you to focus on interpreting results rather than performing tedious row operations manually.
If you want to practice solving matrices or check your work, try the Matrix Row Reduction Calculator for step-by-step solutions.
By mastering RREF, you’ll gain a deeper understanding of linear algebra and how it applies to real-world problem-solving.
Keep practicing, and soon, you’ll be solving even the most complex matrix problems with confidence! 🚀

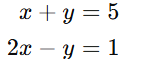
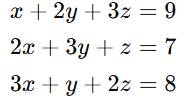
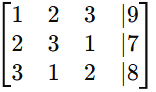
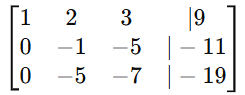
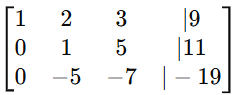
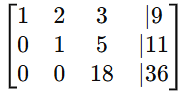
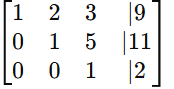
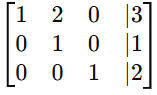
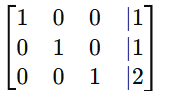
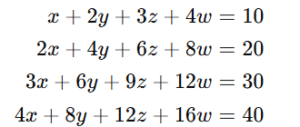
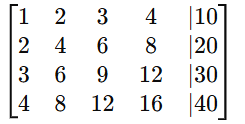
Be First to Comment