A common question students ask is: Is Reduced Row Echelon Form unique?
In other words, if we take the same matrix and apply row operations, will we always end up with the same RREF?
Understanding this concept is crucial because uniqueness ensures that no matter how we reduce a matrix, we always arrive at the same result—making RREF a reliable and powerful tool in mathematics.
When solving systems of linear equations, one of the most important tools in linear algebra is the Reduced Row Echelon Form (RREF) of a matrix.
Reduced Row Echelon Form is a standardized form where each leading coefficient is 1, all other entries in the pivot column are zero, and the pivots move from left to right across the rows. This form is widely used because it allows us to quickly determine solutions to a system.
In this post, we’ll explore why Reduced Row Echelon Form is unique, how it differs from Row Echelon Form (REF), and why this uniqueness makes it useful in applications like solving equations, data science, and engineering.
If you want to experiment with matrices yourself, try using the Matrix Row Reduction Calculator to see RREF in action!
Understanding Row Echelon Form vs. Reduced Row Echelon Form
Before we discuss the uniqueness of Reduced Row Echelon Form (RREF), it’s important to understand how it differs from Row Echelon Form (REF).
Both forms are used in solving systems of equations, but RREF has stricter conditions that make it a fully simplified version of REF.
Key Differences Between REF and RREF
| Feature | Row Echelon Form (REF) | Reduced Row Echelon Form (RREF) |
|---|---|---|
| Leading Coefficients | Must be 1 (pivots) | Must be 1, and every pivot column has all zeros except for the pivot |
| Position of Leading 1s | Each leading 1 is to the right of the one above it | Same as REF |
| Zeros Below Pivots | All zeros below each leading 1 | Same as REF |
| Zeros Above Pivots | Not required | Required (each pivot column must have zeros above and below the leading 1) |
| Solution Clarity | May require back-substitution | Solution is fully simplified |
In our previous blog post on Row Echelon Form vs. Reduced Row Echelon Form, we explored these differences in detail and when to use each form.
The key takeaway is that Reduced Row Echelon Form is the most reduced version of a matrix, meaning it cannot be simplified further.
When Does a Matrix Reach Its Final Form?
A matrix reaches:
✅ REF when it satisfies the first three conditions above.
✅ RREF when it meets all four conditions, including zeros above each pivot.
A matrix can have many possible REF forms, depending on the sequence of row operations used.
However, RREF is always unique—no matter how you reduce a matrix, you will always reach the same RREF.
This brings us to the next section: Why is RREF unique?
The Uniqueness of Reduced Row Echelon Form
One of the most important theorems in linear algebra states:
Every matrix has exactly one Reduced Row Echelon Form, regardless of the sequence of row operations used to obtain it.
This means that while different row operations can be applied in various orders, the final RREF of a matrix will always be the same.
Why Does Every Matrix Have a Unique RREF?
To understand why RREF is unique, consider:
✅ Row Operations Do Not Change Solutions – Since row operations are reversible, they preserve the fundamental relationships between equations in a system.
✅ Pivot Structure is Fixed – Every matrix has a specific set of pivot positions (determined by the rank of the matrix). Since RREF requires zeros above and below every pivot, there’s only one possible arrangement that satisfies all conditions.
✅ Different Paths, Same Destination – You might perform row swaps before scaling, or scale before eliminating entries. However, as long as you apply valid row operations, you’ll always end up with the same RREF.
This uniqueness is why RREF is preferred for solving systems of equations—once you reach the final form, the solution is clear, consistent, and unambiguous.
To see this in action, try reducing matrices using the Matrix Row Reduction Calculator.
No matter what steps you take, you’ll always reach the same RREF!
In the next section, we’ll explore why RREF uniqueness matters in practical applications and how it’s used in real-world problem-solving. 🚀
Proof of Uniqueness
We’ve established that every matrix has exactly one Reduced Row Echelon Form (RREF), but why is this true?
Let’s go through a step-by-step explanation and an example to illustrate this concept.
Step-by-Step Explanation
1️⃣ Row operations preserve equivalence – Elementary row operations (swapping, scaling, and adding multiples of rows) do not change the fundamental relationships in the matrix. This ensures that different row reduction sequences still lead to the same result.
2️⃣ Pivot positions are fixed – The pivot columns of a matrix are determined by its rank. Because RREF requires all leading 1s to be in these fixed pivot positions, no matter how you reduce the matrix, the final placement of these leading 1s is always the same.
3️⃣ Zeros above and below pivots must be enforced – Unlike REF, which allows multiple valid forms, RREF requires each pivot column to have zeros both above and below the leading 1s. This eliminates any alternative final forms.
4️⃣ Conclusion – Since the row reduction process follows strict rules and pivot placement is uniquely determined by the matrix itself, the RREF of any given matrix is always the same, regardless of the row operations used.
Example: Different Paths, Same RREF
Let’s take the matrix:
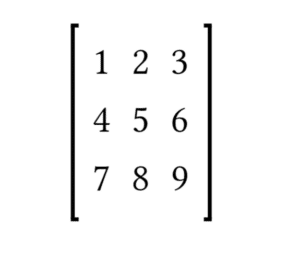
We will perform row reduction using two different paths, but both will lead to the same RREF.
Path 1: Traditional Row Reduction
- Make the first pivot 1 (already done).
- Eliminate entries below it using row operations.
- Normalize the second pivot and eliminate above/below entries.
- Normalize the third pivot and enforce zeros above/below.
Path 2: A Different Sequence
- Swap rows to get a different order.
- Perform row operations in a different sequence.
- Normalize pivots and enforce zeros.
No matter which approach we take, the final RREF will be:
This confirms that RREF is unique, regardless of the path taken.
If you’d like to experiment with different reduction methods, you can use matrixrowreductioncalculator.com to verify this theorem in action!
Applications of Unique Reduced Row Echelon Form
Now that we know RREF is unique, let’s explore why this property is so useful in various mathematical and real-world applications.
1. Solving Systems of Linear Equations
Since RREF is unique, once we reduce an augmented matrix to its RREF, the solution to the system of equations is immediately clear. This eliminates ambiguity and ensures that everyone solving the same system arrives at the same final result.
2. Determining the Rank of a Matrix
The rank of a matrix is the number of nonzero rows in its RREF. Since RREF is unique, the rank of a matrix is always the same, no matter how we perform row reduction. This is crucial in applications like linear regression, machine learning, and optimization problems.
3. Checking Linear Independence of Vectors
If a set of vectors forms the columns of a matrix, reducing the matrix to RREF allows us to check for linear dependence. If any column becomes a zero column in RREF, the vectors are linearly dependent. This has applications in computer graphics, physics, and data science.
4. Finding the Inverse of a Matrix
When calculating a matrix inverse using the Gauss-Jordan elimination method, RREF ensures that we always get the correct inverse (if one exists). This is widely used in engineering, cryptography, and economics.
Why RREF Uniqueness Matters
Without uniqueness, different people could reduce the same matrix in different ways and end up with conflicting solutions.
Thanks to the uniqueness theorem, RREF guarantees consistency and reliability in solving linear algebra problems.
If you want to practice solving matrices, try using the Matrix Row Reduction Calculator to check how different row operations always lead to the same RREF!
When calculating a matrix inverse using the Gauss-Jordan elimination method, RREF ensures that we always get the correct inverse (if one exists). This is widely used in engineering, cryptography, and economics.
Conclusion
Is Reduced Row Echelon Form Unique? Yes.
In this post, we explored the uniqueness of Reduced Row Echelon Form (RREF) and why every matrix has only one RREF, regardless of the sequence of row operations used.
This property is essential because it ensures consistency in solving linear systems, determining rank, and analyzing vector independence.
The uniqueness of RREF is not just a theoretical concept—it has practical applications in computational mathematics, engineering, physics, and software development.
Many algorithms in machine learning, cryptography, and numerical computing rely on matrix row reduction, making the consistency of RREF a critical factor in automated computations.
If you want to experiment with different row reduction paths and verify that they always lead to the same RREF, try using the Matrix Row Reduction Calculator.
It’s a great way to reinforce your understanding and gain hands-on experience with matrix transformations!

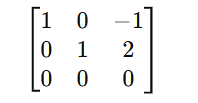
Be First to Comment