If you’ve ever worked with systems of linear equations or matrix algebra, you’ve likely come across Reduced Row Echelon Form (RREF). This special form of a matrix simplifies solving equations, making it a powerful tool in linear algebra. Luckily, you can use a matrix row reduction calculator to calculate reduced row echelon form.
RREF is a standardized way of representing a matrix where each leading entry (pivot) is 1, and all other entries in that column are 0.
Additionally, each leading 1 appears to the right of the leading 1 in the row above it, ensuring a neatly structured form.
This makes calculating reduced row echelon form incredibly useful for solving linear systems, finding inverse matrices, and understanding vector spaces.
In this guide, we’ll break down the step-by-step process to convert a matrix into RREF, helping you master this essential technique with clear explanations and examples.
Then, you can use the free RREF calculator to check your work.
Why Is It Important to Calculate Reduced Row Echelon Form?
1. Solving Systems of Linear Equations
One of the primary uses of RREF is solving systems of linear equations. By transforming a system’s augmented matrix into RREF, you can quickly determine whether the system has a unique solution, infinitely many solutions, or no solution at all.
This is particularly useful in fields like engineering, physics, and computer science, where solving equations efficiently is crucial.
2. Identifying Inconsistencies in a System
When reducing a matrix to RREF, a row of all zeros with a nonzero constant in the augmented column (e.g., 0 0 0 | 1) signals an inconsistent system—meaning there’s no solution. This method provides a straightforward way to check whether a given system of equations is solvable.
3. Finding Matrix Inverses
A square matrix is invertible only if its RREF is the identity matrix. By augmenting a matrix with the identity matrix and applying row reduction, you can determine its inverse, which is essential in many mathematical and computational applications.
4. Understanding Linear Dependence and Rank
RREF helps determine the rank of a matrix—the number of linearly independent rows. This concept is fundamental in linear algebra, as it tells us how much information a matrix contains and whether its rows or columns are dependent on each other.
5. Computational Efficiency with Calculators
While manual row reduction is an essential skill, large matrices can be time-consuming to reduce by hand. Using an online matrix row reduction calculator, such as this one, can speed up the process while ensuring accuracy, especially for complex problems.
Let’s get started!
Step-by-Step Guide to Calculate Reduced Row Echelon Form
Step 1: Understanding Matrix Row Operations
First, to convert a matrix to Reduced Row Echelon Form (RREF), you need to perform three types of row operations:
- Swapping Rows: You can exchange any two rows in the matrix. This is useful when you want to move a row with a leading 1 to the top or position a pivot correctly.
- Multiplying a Row by a Nonzero Scalar: You can multiply an entire row by a nonzero constant to make a leading coefficient 1 (also known as a pivot).
- Adding or Subtracting Rows: You can add or subtract a multiple of one row to another row. This helps eliminate values above and below a pivot, forming the desired RREF structure.
Mastering these operations is essential for row reduction, as they form the foundation for the next steps.
Step 2: Getting the First Pivot to 1
- Locate the first column that contains a nonzero number.
- If needed, swap rows to bring a nonzero value to the top of this column.
- Multiply the row by a scalar so that the leading coefficient becomes 1.
Step 3: Creating Zeros Below the Pivot
- Use row operations to eliminate all values below the leading 1 (pivot) by adding or subtracting multiples of the pivot row.
- This ensures that only the pivot remains in its column.
Step 4: Moving to the Next Pivot
- Move to the next column and repeat the process:
- Find the first nonzero entry.
- Swap rows if necessary.
- Scale the row so the pivot becomes 1.
- Eliminate values below the pivot.
Step 5: Creating Zeros Above the Pivots
- Once all pivots are in place and zeros exist below them, work upwards.
- Use row operations to eliminate any numbers above the pivots, ensuring that each pivot is the only nonzero value in its column.
Step 6: Calculate Reduced Row Echelon Form
A matrix is in Reduced Row Echelon Form when:
- Each pivot is 1, and it is the only nonzero entry in its column.
- The pivots move from left to right as you go down the rows.
- Any row of all zeros (if present) is at the bottom of the matrix.
For larger matrices, this process can be tedious. Using a row reduction calculator can help verify results quickly.
Example: Calculate Reduced Row Echelon Form Using a Matrix Row Reduction Calculator
Let’s start with a simple 2 x 3 augmented matrix:
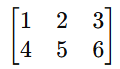
Step 1: Enter the Matrix into the Calculator
- Go to Matrix Row Reduction Calculator.
- Input the matrix values:
- First row: 1, 2, 3
- Second row: 4, 5, 6
- Click Calculate RREF to begin row reduction.
Step 2: The Calculator Performs Row Operations
The tool will apply row operations automatically, but let’s manually verify the steps:
Row Operation 1: Make the First Pivot 1
Our first pivot is already 1 in row 1, so no changes are needed.
Row Operation 2: Eliminate Below the Pivot
To create a 0 below the pivot (first column, second row), subtract 4 × Row 1 from Row 2:
This gives us:
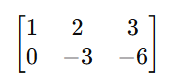
Row Operation 3: Make the Second Pivot 1
Divide Row 2 by -3 to make the second pivot 1:
Resulting in:
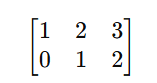
Row Operation 4: Eliminate Above the Pivot
To ensure the second column has a 0 above the pivot, subtract 2 × Row 2 from Row 1:
Final RREF form:
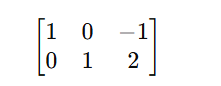
Step 3: Verify the Result with the Calculator
After completing these steps manually, compare your answer with the result given by the Matrix Row Reduction Calculator. If they match, you’ve successfully reduced the matrix!
Conclusion
Understanding how to transform a matrix into Reduced Row Echelon Form (RREF) is an essential skill in linear algebra. We covered:
- The importance of RREF in solving systems of equations
- The three fundamental row operations
- A step-by-step process to achieve RREF
- A practical example using a matrix row reduction calculator to verify results
Now, it’s your turn! Try solving a few matrices on your own using the steps outlined in this guide or trying out some more Row Echelon Form Examples.
If you need help checking your work, use the Matrix Row Reduction Calculator to confirm your results. The more you practice, the more intuitive row reduction will become and the easier it will be to calculate reduced row echelon form!

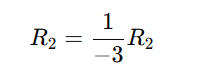
Be First to Comment